抢红包在现在是个很常见的业务了,常见到公司的产品们也想着拍个脑门上一个这种功能,于是调研了下目前常用到抢红包技术方案,也产生了一些问题,记录下来。
抢红包业务流程
用户在一个群体中发一个总价值X的『红包』,此『红包』可以划分出N个,每个『子红包』会产生出一个随机价值,N个的总价值=X,此群体中的人可以『抢』这N个子红包,每人最多可抢一个,抢到者可以给自己账户增加和『子红包』相同的价值,先来先得,抢完为止。
抢红包业务关注点
并发问题:1个包含10个子红包的红包可能同时会有1000个人抢,必然产生并发问题
随机问题:保证每个子红包的价值足够随机,且每个子红包价值在统计上概率是相同的
和秒杀问题的关系
网上有很多文章将抢红包和秒杀做对比,并且在很多地方都使用了解决秒杀问题的方案,但是我看下来感觉一些地方是有些生搬硬套的。从头捋一下两者的相同和不同点才能看哪些能用哪些不能
相同点:
- 并发问题,秒杀也是多人抢少量东西,产生大量并发
不同点:
- 流量问题,秒杀带来的流量问题要比抢红包更大,更偏向于做活动之类的暂时性业务,绝大部分流量是重复请求,因为即然是秒杀所以他可以使用很多削流量的方案,可以限流,可以加各种缓存,甚至可以根据用户运气先把运气不好的用户请求打回来,让你开心的点点点觉得自己马上就能抢到了,最后还可以使用队列方式让你排队。但抢红包并不会带来直线上升的流量增长,更多的是日常业务持续的流量
- 超卖问题,秒杀可能会带来超卖问题,100个商品可能最终卖了102个,这对于秒杀业务是可以接受的,但对于红包问题,不能发了10个红包,被人抢走12个,还要让发红包的再补2块钱或者平台自己拿2块钱补上
- 并发侧重点不同,秒杀像100万人要进1个房间,抢房间里的苹果手机,抢红包更像是100万人进了1万个房间,每个房间的人抢房间里各自的1块钱,同样的100万人,同样价值1万块的东西,100万人同时开抢,但一个是要保证100万人抢进一个房间别出错,一个是要保证这1万个房间里面的100个人别出错。当然12306更复杂,属于是100万人同时进一个房间秒杀1万个不同的红包,边抢里面管理员边发新的边收回失效的,还不让超卖。
基于上面,我觉得,我们不能把抢红包的重点放在削流量上
红包生成方案
红包生成可以划分为两种
- 一种是预先生成,我要发10个总共100块钱的红包,我先把它随机分成10个份,每份里放一个随机价值,存下来,有人抢时,我直接从里面拿一个发给他,发完为止。这种好处是抢红包时不需要临时计算,但有临时数据需要存储
- 另一种是实时生成,我要发10个总共100块钱的红包,有人来抢时,我随机一个数,从100块钱里拿对应的发给他,直到第10个来,正好把手里的钱发完。这种好处是省了存储,但多了在并发时的计算资源
看上去是用空间换时间还是时间换空间的方案,但实际代码逻辑上两者对于锁的依赖不同:
预生成
发红包:1次DB写+1次redis(push)
抢红包:1次DB读(可省略)+1次redis(pop)+1次DB写(可异步)
实时生成
发红包:1次DB写
抢红包:1次DB读+1次DB写(同步)+锁(自旋)
发红包不属于高频操作,也不存在并发问题,可不考虑,主要考虑抢红包场景
对于预生成,在不考虑用cache抗流量的情况下,在抢红包时会有一个读DB(这一步实际可以省略),一个redis的pop,一个写db的操作,不过写db实际上可以做成异步的,因为在redis操作时实际上已经扣减的红包;实时生成是一个读DB+一个写DB,在并发情况下生成时读取红包余额和计算红包数+写回是会有冲突出现的,所以需要加锁或直接走排队,无论哪种方案,都会增加复杂度和维护难度,而且对于并发能力也有影响。而预生成无论是弹出红包还是写抢红包记录都是可并发操作的,如果担心逻辑中断丢失,最多再加个事物,但事物是两种方案都会有的问题,而且我觉得,如果没有超高的实时性要求,那走一套旁路对账的方式,完全可以及时发现并处理问题,没必要用事物去压性能。
随机方式
除了架构的方案,还有红包本身的随机方式,随机应该有两个要求
- 每个用户最少能拿到0.01元
- 每个用户获得的红包金额期望应该是一致的,也就是 红包总价值/红包个数
最简单的随机方式肯定是
$$ F_{(x)} = \begin{cases} random(0.01, total) & (x=1) \\ random(0.01,total - \sum_{i=1}^{x-1}f_{(i)}) & (x!=1) \end{cases} $$ 比如第1个人从0.01到100随机一个15,那第二个人就从0.01到85随机,但这样会导致前面的人拿的多,越往后拿的越少,每个人概率不一样,不太考虑查到网上常用的是2倍随机法,就是每个人从上一个人抢完后省下的钱里拿自己平均数的2倍来做为上限去随机,比如还是100块钱10个人分,我们先忽略掉每人最少0.01的限制,每个人平均应该分到10块钱,那第1个人就从0到(100/10)*2作为随机范围,如果也抢到15,那后面的人就以(100-15)/9*2来当上限。网上都说这种算法是平均的,那我怎么算他的期望呢?好问题,问下deepseek去吧,我不记得期望怎么递归计算了。
我们直接跑个test不就行了。
func Test2Avg(t *testing.T) {
var rs map[int]int = make(map[int]int, 10)
for range 1000000 {
var sum int = 100
for c := range 10 {
if c == 9 {
rs[c] += sum
break
}
maxUp := int(math.Round(2*100*float64(sum)/(10-float64(c))/100.0) - 1)
t := rand.IntN(maxUp) + 1
sum -= t
rs[c] += t
}
}
for i := range 10 {
fmt.Println(rs[i])
}
}
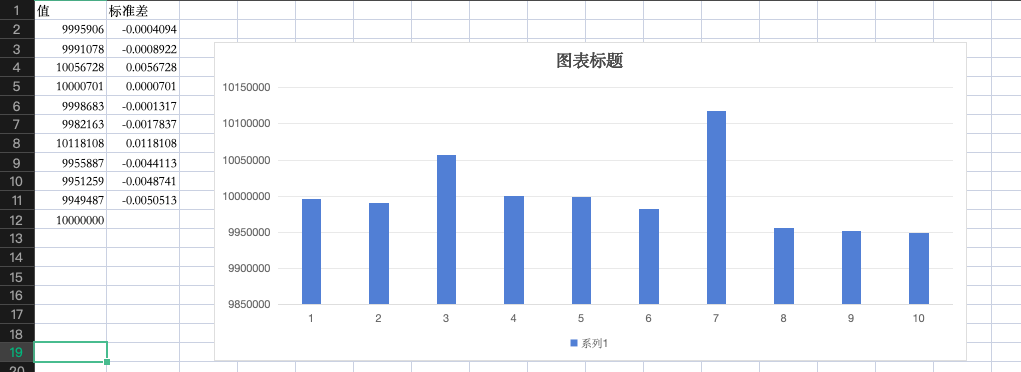
100万次随机后可以看到10个人抢到的红包总数差距非常小,虽然结果出来因为整数换算问题会有一点点不公平(比如前3个和第6位总比其它位置数值高),但公差不超过1%,而且如果是预生成的话,我们shuffle下可以认为是不影响的。
总体伪代码如下,(不包含对账和转账)
void sendRedPacket(int userId, int money, int count) {
//保存红包数据入库
redPacketId = saveRedPacketInfoToDB(userId, money, count);
//预生成子红包列表
redPacketList = generateRedPacketList(money, count);
//预生成红包列表入redis队列
redis.ush(sprintf("red_packet:%d", redPacketId, redPacketList);
//通知群用户红包生效
sendRedPacketMsg(redPacketId);
}
int* generateRedPacketList(int money, int count) {
rs = (*int)malloc(count*sizeof(int))
//生成count个子红包
for (int i = 0; i++; i < count) {
//最后一个人takeAll
if (i == count - 1) {
rs[i] = money;
return rs
}
//2倍均值法
spCount = random(0, (money/count - i)*2);
money -= spCount;
rs[i] = spCount;
}
return rs
}
int grabRedPacket(int userId, int redPacketId) {
redPacketInfo = readRedPacketInfoFromDB(redPacketInfo);
//判断是不是生效中的红包,需要有对账来修改红包状态
if (redPacketInfo.Status != valid) {
return 0
}
//从预生成的子红包队列里弹一个出来
money = redis.pop(sprintf("red_packet:%d", redPacketId));
//money==0说明红包抢完了,但对账还未把状态改过来,极端概率情况
if money == 0 {
return 0
}
//用户抢红包记录写表
writeGrabRedPacketRecordToDB(userId, redPacketId, money);
}
关于网上流传的微信红包方案
选定架构方案和算法方法后整体基本就敲定了,不过我在查技术方案时看到之前网上流传的微信负责红包的相关同学的文章,提到了微信的红包技术方案,他们选的是实时计算,表示是实时计算不需要临时存储,速度快,而且为了解并发冲突,还走了个hash分流的方案。我只能说,对于技术方案的选型,我们还是要深入分析优劣再自己做结论。
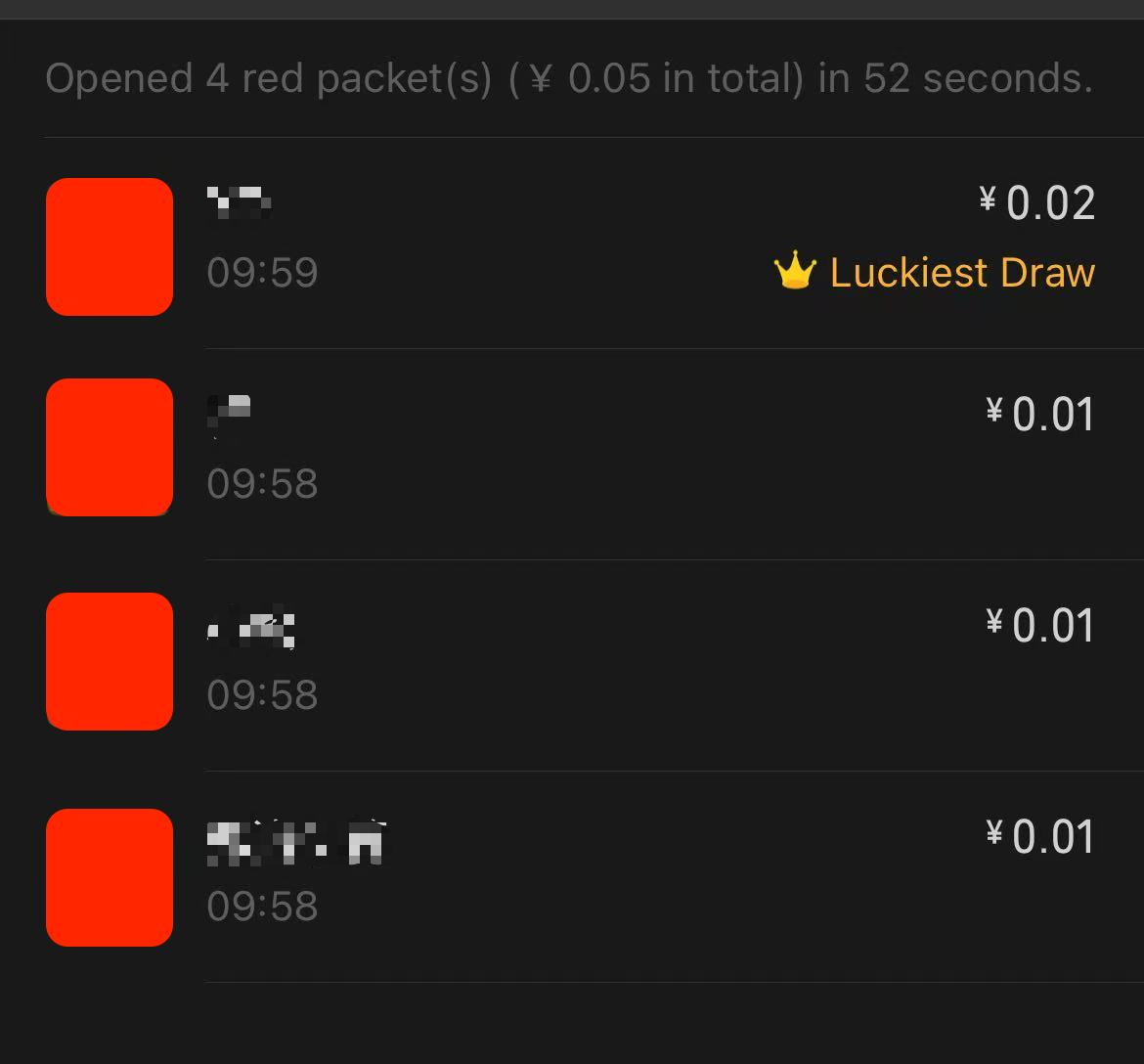
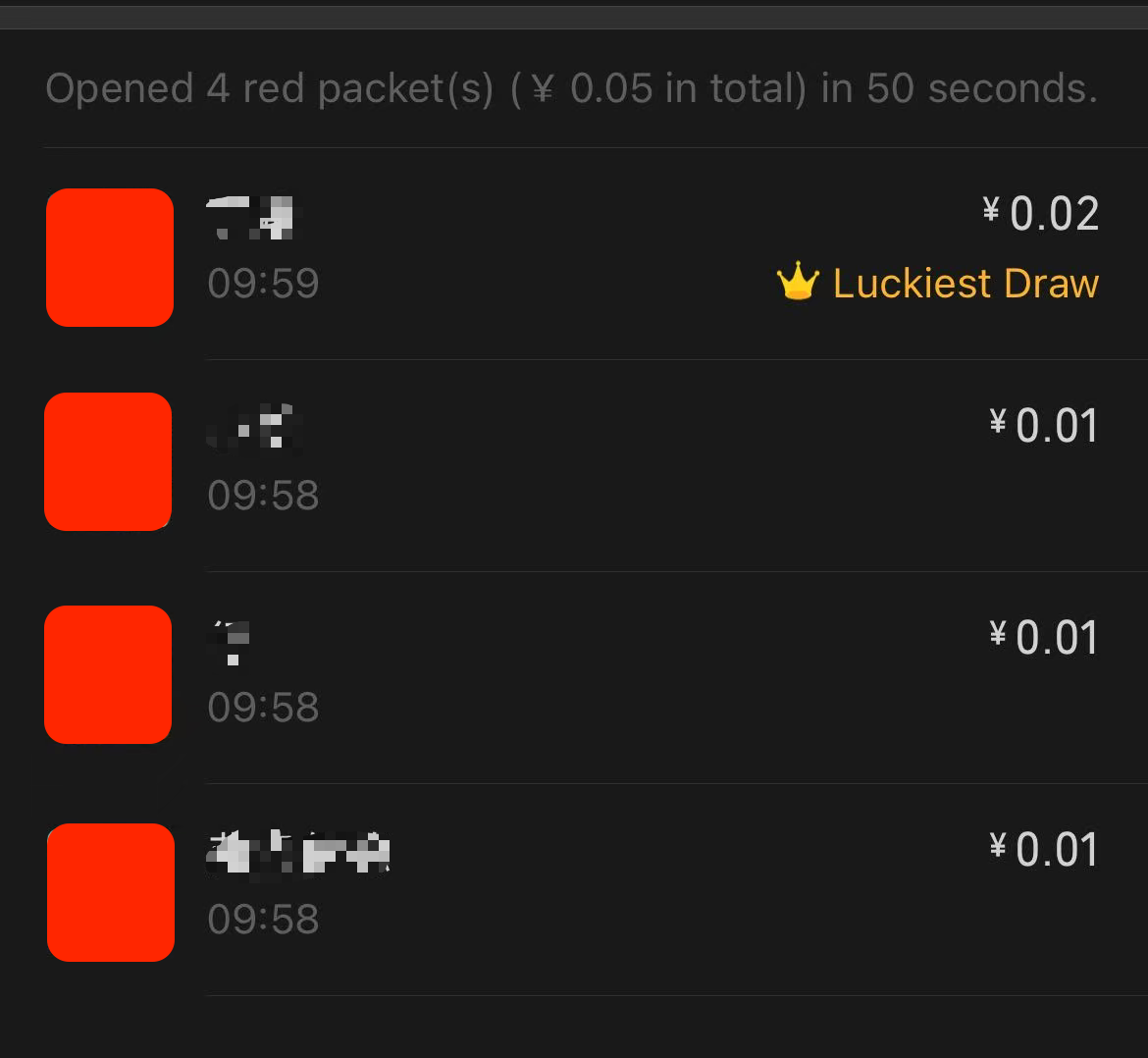
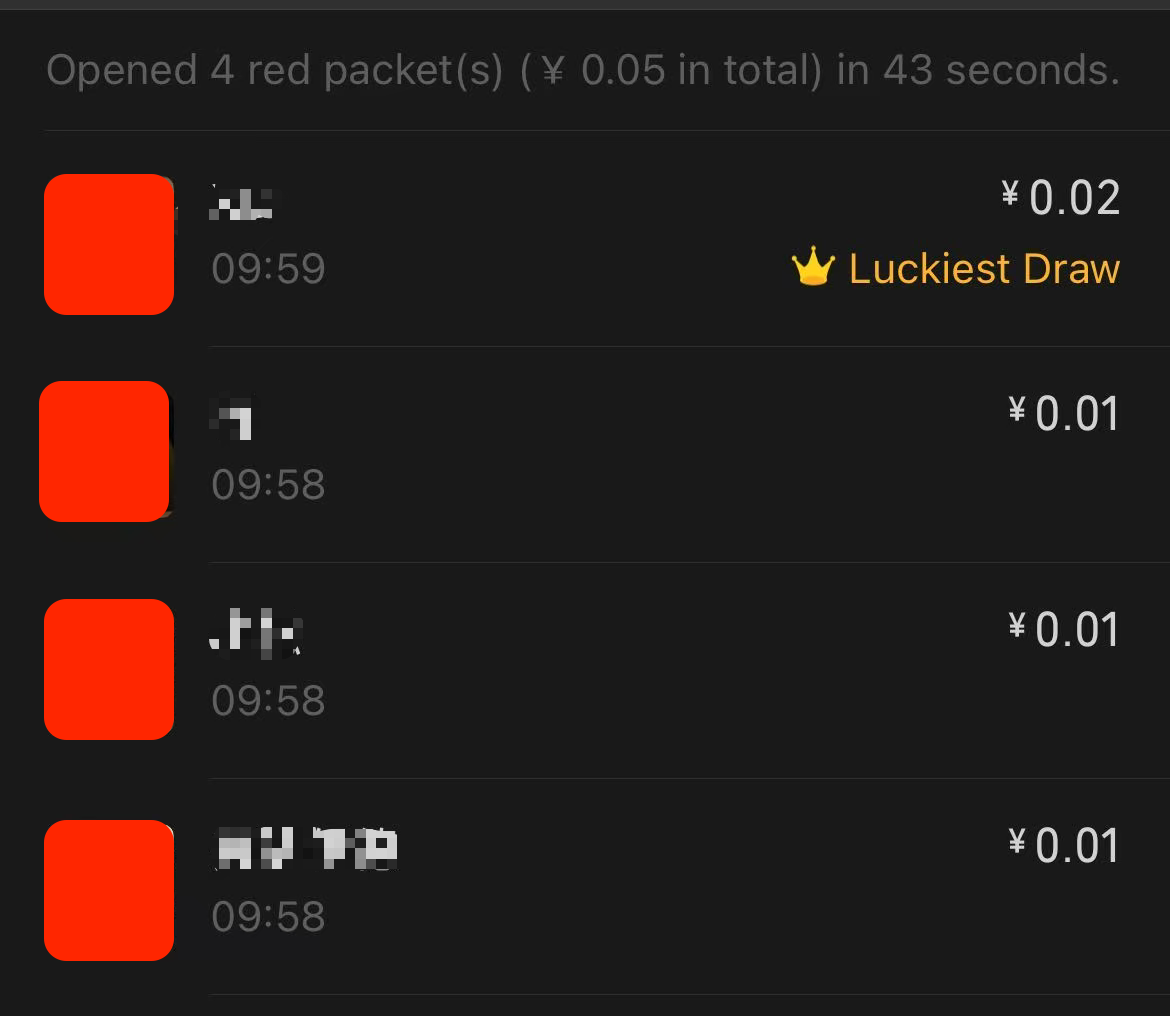
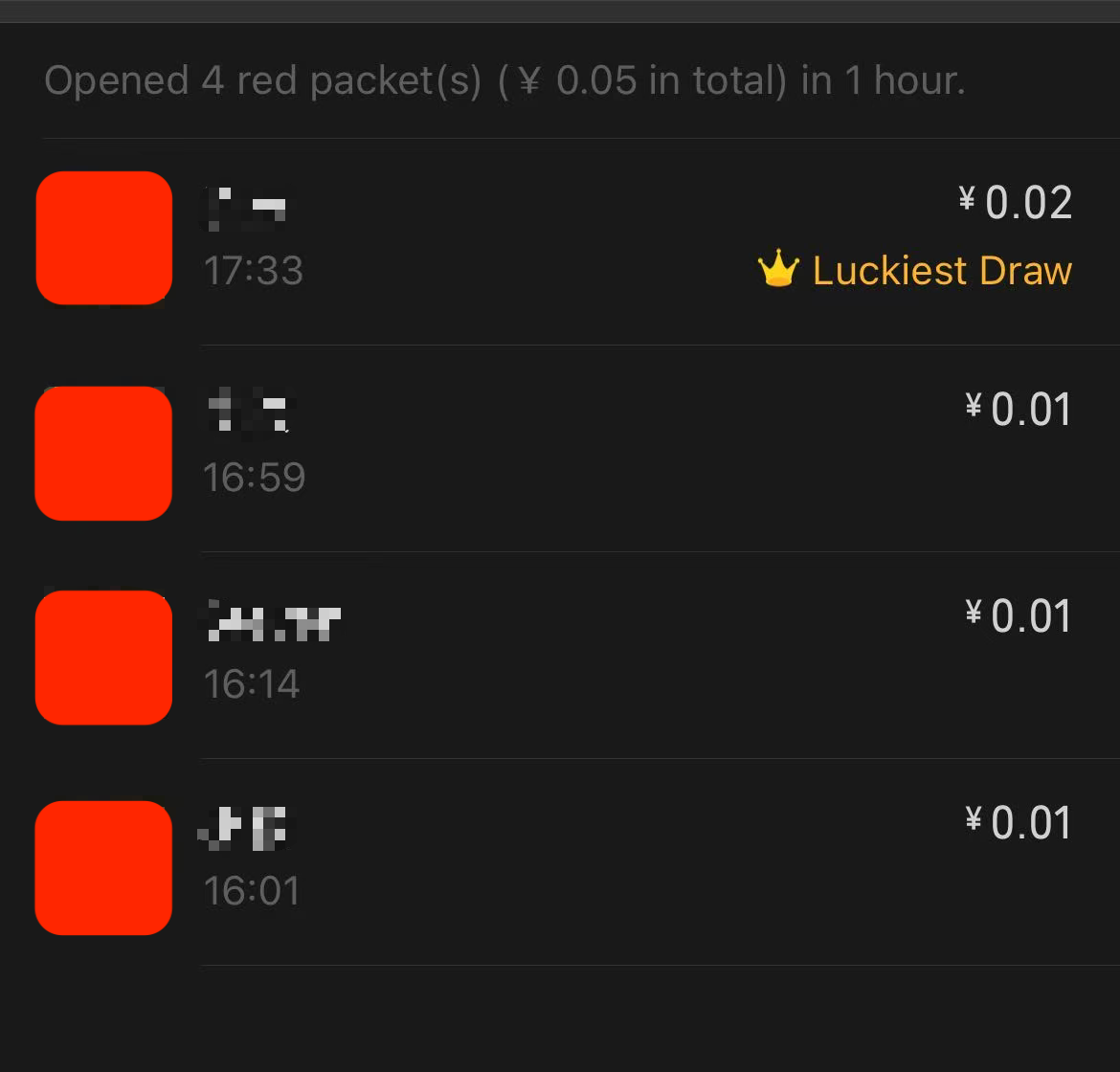
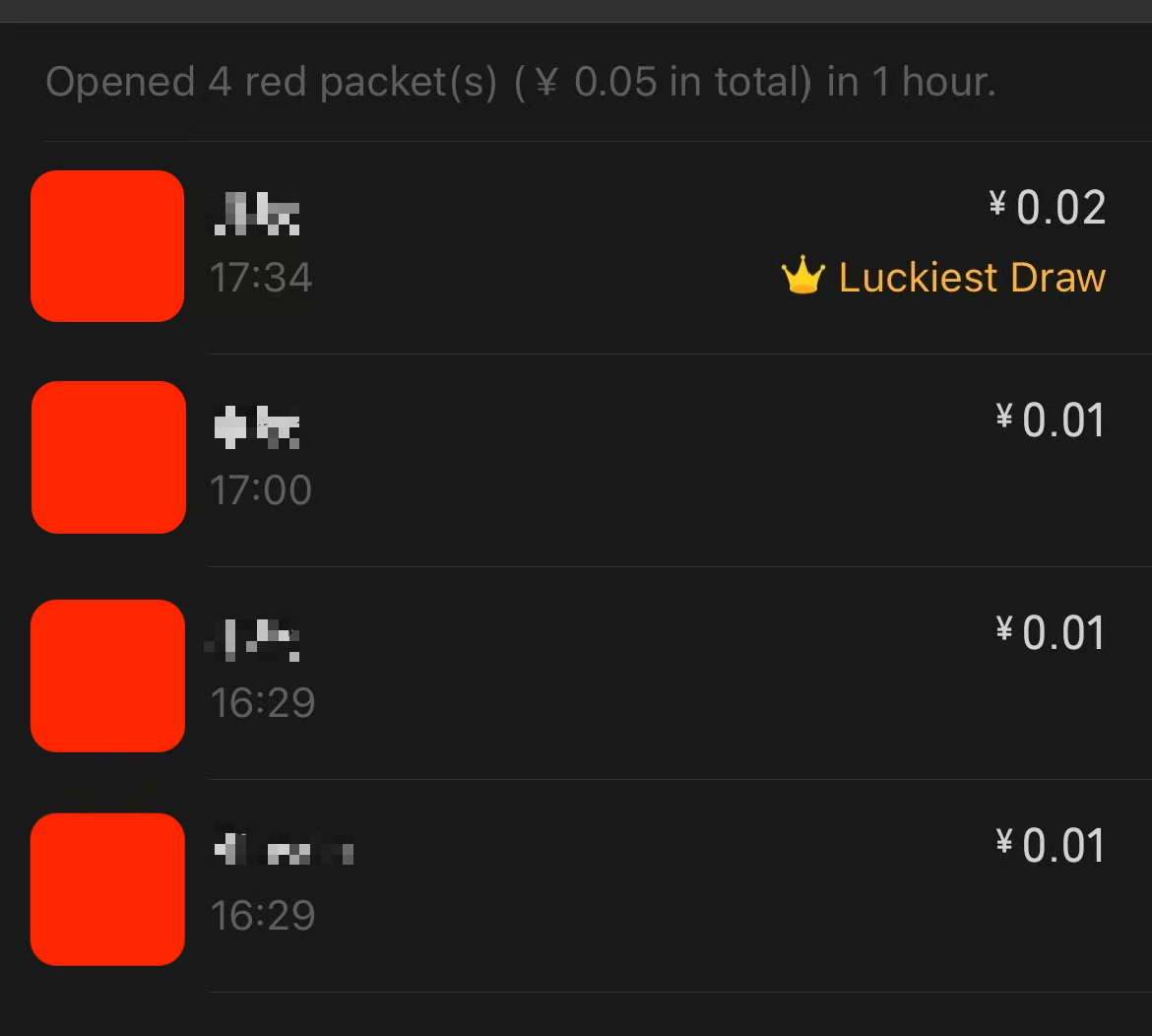
2倍均值有个卡bug的方式可以看出来,比如我们发0.05给4个人,就会固定出现3个0.01和1个0.02,根据2倍均值的算法,0.02会固定出现在最后一个子红包上,比如下面就是给4个人发100个,每个0.05元的红包后4个人抢完后的总价值,可以看到第4个人总共抢了2块钱,说明他每次都是0.02
以下是我花了2毛5得出来的微信使用2倍均值的结论